Генерация случайных полигонов в C#

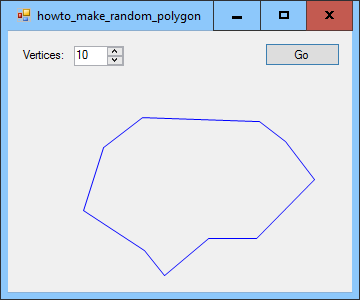Мне нужен был метод генерации случайных полигонов для графической программы, и следующий код показывает результат.

// Создаем случайные многоугольники внутри ограничивающего прямоугольника.
private static Random rand = new Random();
public static PointF[] MakeRandomPolygon(
    int num_vertices, Rectangle bounds)
{
    // Выбор случайных радиусов.
    double[] radii = new double[num_vertices];
    const double min_radius = 0.5;
    const double max_radius = 1.0;
    for (int i = 0; i < num_vertices; i++)
    {
        radii[i] = rand.NextDouble(min_radius, max_radius);
    }

    // Выбор случайных угловых весов.
    double[] angle_weights = new double[num_vertices];
    const double min_weight = 1.0;
    const double max_weight = 10.0;
    double total_weight = 0;
    for (int i = 0; i < num_vertices; i++)
    {
        angle_weights[i] = rand.NextDouble(min_weight, max_weight);
        total_weight += angle_weights[i];
    }

    // Преобразование весов во фракции 2 * Pi радианов.
    double[] angles = new double[num_vertices];
    double to_radians = 2 * Math.PI / total_weight;
    for (int i = 0; i < num_vertices; i++)
    {
        angles[i] = angle_weights[i] * to_radians;
    }

    // Вычислить местоположения точек.
    PointF[] points = new PointF[num_vertices];
    float rx = bounds.Width / 2f;
    float ry = bounds.Height / 2f;
    float cx = bounds.MidX();
    float cy = bounds.MidY();
    double theta = 0;
    for (int i = 0; i < num_vertices; i++)
    {
        points[i] = new PointF(
            cx + (int)(rx * radii[i] * Math.Cos(theta)),
            cy + (int)(ry * radii[i] * Math.Sin(theta)));
        theta += angles[i];
    }

   // Вернем точки.
    return points;
}

Основная идея заключается в создании точек для случайных полигонов на основе тех, которые лежат на эллипсе в пределах границ, заданных в качестве параметра. Углы точек вокруг эллипса и их расстояния от центра случайным образом изменяются для создания случайного многоугольника.

Сначала код выбирает случайные радиусы для точек в диапазоне от 0,5 до 1,0. Это достаточно просто. (Информацию о методе расширения NextDouble класса Random см. В разделе Создание методов расширения для генерации случайных чисел двойной точности в C#.)

Затем код генерирует случайные углы для точек. К сожалению, эта часть немного сложнее.

В конечном итоге программе нужны углы между 0 и 2π радианами, и они нуждаются в них в отсортированном порядке. Для генерации углов код сначала выбирает случайную «нагрузку» между 1.0 и 10.0 для каждой точки. Код отслеживает общее количество значений в переменной total_weight.

Затем программа обрабатывает каждое из значений как долю от всего 2π радианов в эллипсе. Угол каждой точки представляет собой угол между этой точкой и предыдущей точкой, и он использует нагрузку для определения фракции. Например, предположим, что угол четвертой точки равен 3, а сумма всех углов равна 20. Тогда угол между третьей и четвертой точками должен быть (3/20) * 2π радиан.

Чтобы преобразовать значения в углы, программа проходит через значение и преобразует каждое в угол, умножая каждый угол на 2 * Math.PI / total_weight.

(Я думал о более простом способе генерации углов: выбирайте случайные значения между 2π радианами, а затем сортируйте их. К сожалению, это может привести к некоторым дублирующимся значениям или значениям, которые очень близки друг к другу, и это даст многоугольные уродливые всплески. Показанный здесь, более сложный, но создает верхнюю и нижнюю границы на величину, на которой углы смежных точек могут отличаться.)

Наконец, код использует углы и радиусы для вычисления положения каждой точки. Он использует методы расширения класса MidX и MidY класса Rectangle, чтобы найти среднюю точку границ. (См. Раздел «Создание методов расширения прямоугольника на C#» для получения информации об этих методах.)

Программа использует Math.Sin и Math.Cos для определения направления смещения для каждой точки, умножается на радиусы X и Y ограничивающего эллипса, а затем умножается на случайный радиус точки, чтобы получить конечное местоположение.

Затем метод просто возвращает точки в массиве, поэтому вызывающий код может использовать метод DrawPolygon объекта Graphics для его рисования.

Источник: csharphelper.com/blog/2017/07/generate-random-polygons-in-c/

(2 оценок, среднее: 4,50 из 5)